Rewriting the textbook: covered interest parity

                “Toto, I’ve a feeling we’re not in Kansas anymore.” Dorothy in The Wizard of Oz

For decades, textbooks on international economics and finance built a part of their scaffolding on the foundation of a relationship called covered interest parity (CIP). CIP postulates that, in a world of free capital flows, currency-hedged returns on equivalent-risk assets will equalize across countries. For example, the return to investing in a 1-year U.S. Treasury bill will equal the return to purchasing euros, investing the proceeds in a 1-year German Government liability, and purchasing a contract guaranteeing the future euro/dollar exchange rate at which the euros will be converted back to dollars a year later. In practice, the CIP relationship was such a reliable feature of international fixed-income markets that for decades one could think of banks operating a nearly costless CIP machine to perform what many viewed as a riskless arbitrage.

Then, one day, the CIP machine broke down. It first stopped working in the Great Financial Crisis (GFC) of 2007-2009, when counterparty and liquidity risks both skyrocketed, raising the possibility of defaults and losses in executing the trades necessary. That is, CIP was not a riskless arbitrage. (For a broad analytical and historical perspective on interest parity, see Levich.)

As a wave of recent research highlights (see, for example, here and here), the conventional, pre-crisis model of the CIP machine remains impaired even as the counterparty and liquidity risks that characterized the GFC have receded. Borio et al suggest two related reasons for the breakdown: (1) intermediaries’ funding requirements in some currencies (notably U.S. dollars) creates a powerful need for hedging currency risk; and (2) intermediaries now find it much more expensive to expand their balance sheets as required to execute the underlying CIP transactions. That is, there is both an increase in demand and a reduction in supply. Put differently, balance sheet costs appear to have created limits to arbitrage in currency markets even when counterparty, liquidity and other risks are not present.

The persistent CIP breakdown has prompted worries that, because of intermediaries’ limited capital and resulting constraints on the size of their balance sheet, market liquidity will be even scarcer in future episodes of financial stress. While that may be so, another possibility is that intermediaries now engage in better management of their capital, which they previously exploited to support a range of activities—including the CIP trades of clients (such as hedge funds)—without adequate compensation. If that is the case, then we might expect a reduction in the frequency and amplitude of financial stress episodes.

Either way, it is past time to re-write the textbooks. So, here goes.

Let’s begin by defining CIP in a simple context of two currency areas (call them U.S. dollars and euros) each with an equivalently default-free, liquid asset that has a one-year maturity (call these U.S. Treasurys and German Bunds). The return after one year on the safe dollar asset is (1+r) while the return on the safe euro asset is (1+r*). Suppose you have $1 to invest and can choose between the two assets. If you invest in the U.S. Treasury, you receive (1+r) dollars after one year. To invest in the German Bund without incurring foreign exchange risk, you must first convert your dollar into euros at the spot exchange rate of U.S. dollars per euro ( S$/€ ) and simultaneously contract with a bank to convert the future euro proceeds back into dollars at the one-year forward exchange rate ( F$/€ ). By using today’s forward exchange rate, you hedge (“cover”) the exchange rate risk in this transaction.

Assuming there is no risk in the forward transaction with the bank, you will be indifferent between the two investments only if the following CIP relationship holds:

The left-hand side is the return on the $1 invested in the U.S. asset. On the right-hand side, the first term is the number of euros that you have to invest at the start of the period. The product of the first two terms is the number of euros that you receive after a year. And the final term is the forward rate (known today) at which the euros received in one year (also known today) will be converted to dollars.

With a little bit of algebra, and using a (logarithmic) approximation, we can simplify equation (1) to get:

The left-hand side is the interest rate differential between the two currency regions—the U.S. Treasury rate minus the German Bund rate. The right-hand side is known as the forward premium (f), which equals the ratio of the forward exchange rate (F) divided by the spot exchange rate (S) minus one.

The important thing to realize is that, whenever the left- and right-hand sides of equation (2) are out of whack, intermediaries can profit. If the interest rate differential (r-r*) is smaller than the forward premium (f), a bank can benefit by selling dollars for euros, investing in the euro asset, and hedging by purchasing dollars in the forward market. This causes the dollar to depreciate in the spot market (S$/€ rises) and to appreciate in the forward market ( F$/€ falls), lowering f. Doing this rapidly and without limit (that is, without respect to the size of banks’ balance sheet or cost of capital), depresses the forward premium so that equation (2) holds.

From the early 1970s, when the period of floating exchange rates began, until the financial crisis, CIP deviations were indeed very small and temporary. In practice, intermediaries in the foreign exchange markets, primarily large banks, operated their CIP machines both in money markets and in deep, liquid derivatives markets, such as the cross-currency basis swap market. In this swap market, traders exchange the returns on claims in the two currencies as well as the principal at the start and end of the trade (for a complete description, see Du, Tepper and Verdelhan). And, the spread that swap parties pay to receive dollar cash flows in exchange for euro cash flows is the cross-currency basis (b), defined as:

You can think of b as the difference between the U.S. interest rate (r) and a synthetic dollar interest rate (r*-f) received from a euro-denominated investment. As you can see from equation (2), b is also a direct measure of deviations from CIP. When b=0, CIP holds; otherwise, CIP is violated.

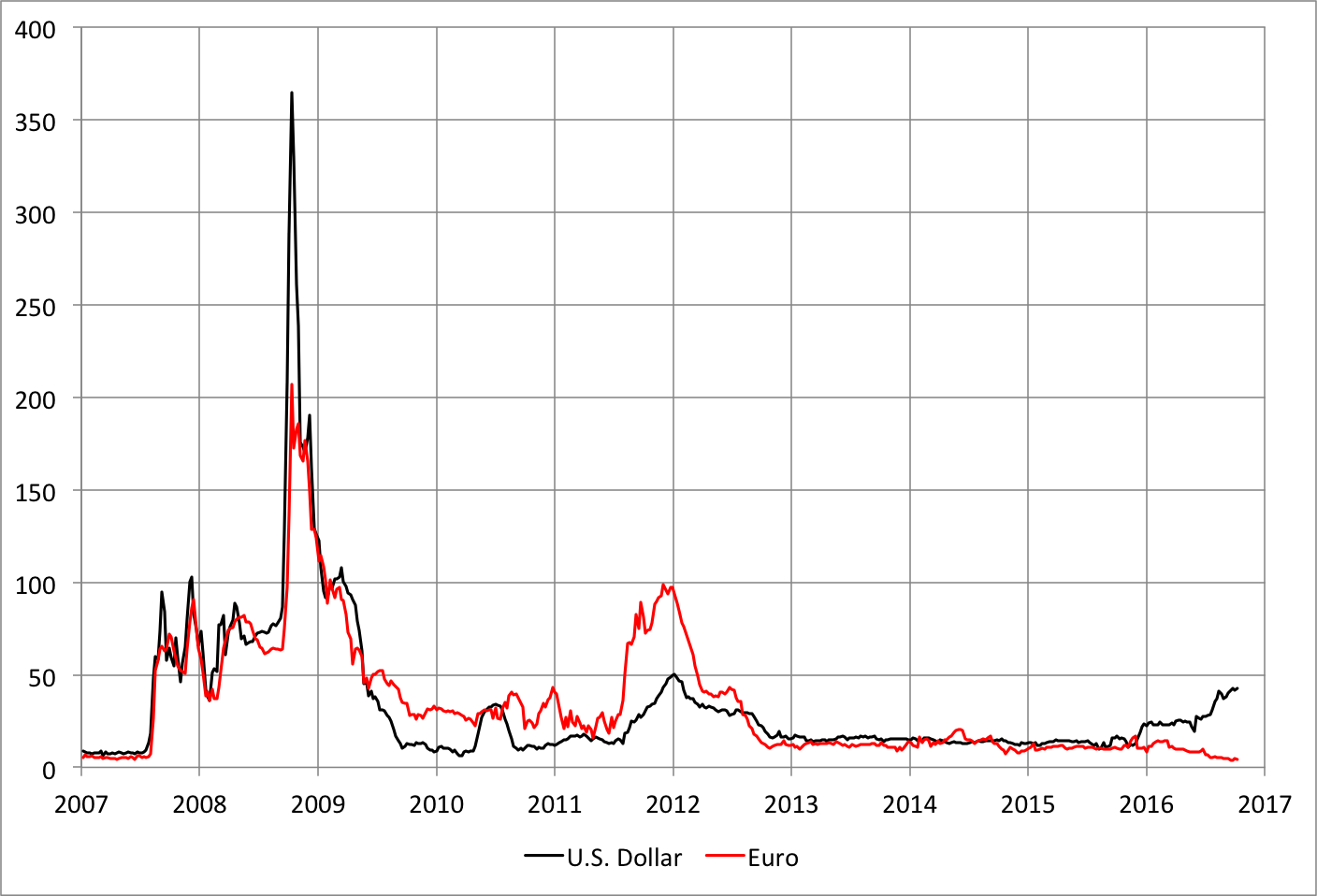
The following figure shows the evolution of the basis (b) since 2005 for one-year dollar/euro and dollar/yen swap contracts (based on LIBOR interest rates). As indicated, there was little or no violation prior to the crisis. CIP was widely perceived as a risk-free arbitrage, so b stayed very close to zero. During the 2007-09 crisis, however, and again during the euro-area crisis, CIP deviations arose across a wide range of currencies (see, for example, Baba and Packer).

Deviations from covered interest parity: one-year cross-currency basis swap (weekly, basis points), 2005-October 7, 2016

Source: Bloomberg.

To understand why financial crises give rise to extraordinary CIP violations, keep in mind that the transactions required to make equation (2) hold require intermediaries to accept counterparty risk—the possibility that their trading partners will be unable to meet their obligations. In both the 2007-2009 crisis and the euro-area crisis, worries about counterparty solvency undermined the ability of intermediaries to borrow to fund assets on the balance sheet (or to expand the balance sheet). They also faced elevated market liquidity risk—it became more difficult and more expensive to sell assets (especially longer maturities) quickly. This mix of elevated counterparty and liquidity risks explains the pattern in the following chart, which plots the spreads between the three-month bank funding rates (which includes both risks) and the three-month overnight indexed swap (OIS) rates (which largely excludes these risks) for both U.S. dollars and euros. Both spreads peaked following the Lehman collapse in 2008 and rose again (albeit less so) in 2011-12 during the euro-area crisis.

U.S. LIBOR-OIS spread and Euribor-OIS spread (basis points, weekly), 2007-October 7, 2016

Note: The maturity is three months. Source: Bloomberg.

So, it is fairly easy to explain CIP violations in 2008 and again in 2011-12. The larger puzzle is what happened beginning in early 2014. Looking back at the first chart, we see that the dollar/yen basis (the red line) has recently reached levels not seen during the two crises. This is where the “limits to arbitrage” story likely plays a role.

It is no surprise that non-U.S. intermediaries lacking a dollar deposit base rely heavily on wholesale dollar funding: in an earlier post, we noted that the scale of dollar intermediation outside the United States exceeds the liabilities of banks operating within the country (as McGuire and von Peter first pointed out in 2009 at the height of the crisis). Now, when Japanese or European banks need dollars, one approach is for them to borrow in their domestic currencies and swap the proceeds into dollars using the cross-currency swap market. From equation (3), the negative currency swap basis (b) for both euros and yen since 2008 tells us that the synthetic dollar interest rate (r*-f) exceeds the cost of borrowing directly in dollars (r). Absent counterparty and liquidity risks, this creates an arbitrage opportunity.

Why should one believe that balance sheet limitations (and the cost of intermediary capital) account for these post-2014 CIP deviations? Du, Tepper and Verdelhan provide a range of evidence for the “limits to arbitrage” hypothesis, including the following:

• increases in estimated regulatory capital charges on long-term CIP trades;
• larger CIP deviations at quarter-end when intermediaries aim to hit leverage targets; and
• compared to LIBOR differentials, CIP deviations are smaller when based on the differentials between the interest rates paid by various central banks on excess reserves (IOER rates), which may be a useful proxy for bank opportunity costs.

To these, Borio et al. would add that reduced funding from U.S. money market mutual funds (MMMFs) since 2015 has boosted foreign bank reliance on the cross-currency swap market as a source of dollars.  And they find that quarter-end spikes in the basis and in repo rates have become more prominent since 2014.

This leads us to two conclusions relevant for the textbook revision. First, despite free cross-border movement of capital, CIP was never a true arbitrage unless one assumed away counterparty and liquidity risks (see, for example, Keynes’ 1923 A Tract on Monetary Reform, pages 124-127, which also describes limits to arbitrage). Second, even in the absence of such risks, CIP trades require the use of capital that is now more costly than it once was. What this means is that the deviations from CIP are likely to rise both with the demand for wholesale funding in foreign currencies (which raises hedging needs) and with the cost of expanding balance sheets. While profit opportunities already may be luring nonbanks to use their capital to substitute for banks’ role in CIP trades, such arbitrage has been insufficient so far to limit CIP deviations.

With respect to CIP, we are not in Kansas anymore. But, unlike Dorothy, it’s doubtful that we will get home again.

Acknowledgement: We are grateful to our friend and NYU Stern colleague, Richard Levich, for his excellent suggestions.